- Yazar admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:29.
- Son düzenleme 2025-01-23 15:39.

Altın Oranın örneklerine klasik mimaride, sanat eserlerinde, doğada ve hatta müzikte her yerde rastlamak mümkündür. İlahi Oran olarak da bilinen bu orantı ifadesi, hem doğal hem de insan yapımı tasarımlarda irrasyonel bir sayının (1.618) uygulanmasıyla uyumlu bir kompozisyon sunar. Büyük ihtimalle Altın Oran'ın güzelliğinin ardındaki matematikten haberiniz yok çünkü Altın Oran, herhangi bir açıklamaya ihtiyaç duymadan doğal olarak hoşunuza gidecek nesneler ve müzikler üretiyor.
Mimaride Altın Oran
Altın Oran, doğada ve sanatta mükemmele yakın bir güzellik yaratır. Günlük yaşamda Altın Oran örneklerini aramaya başladığınızda, birçok anıtsal yapı ve yapı oluşturmak için kullanıldığı durumlar sizi şaşırtabilir. Mimaride Altın Oran kullanıldığında binanın "kutsal mimari" kullanılarak yaratıldığı söylenir. Mimarlar ve tasarımcılar, Altın Oran hesaplamasını bir kareye uygulayarak, insan gözüne estetik açıdan en hoş gelen oranlara sahip olduğuna inanılan Altın Dikdörtgeni oluşturabiliyorlar.
Altın Dikdörtgen Örneği: Parthenon

Yunan heykeltıraş Phidias, özellikle Parthenon sütunlarının hemen üstüne heykel yaptığı bantlarla çalışmaya başladığında, çalışmalarında Altın Oran'ı kullanmıştır. Altın Oran'a atanan sayısal değer olan Phi'nin onun onuruna verildiğini de belirtmek gerekir.
Parthenon'un dış cephesinin boyutlarını ölçerseniz, onun yalnızca Altın Dikdörtgen oluşturmadığını, aynı zamanda sütunlar arasında birçok Altın Dikdörtgen bulunduğunu da keşfedeceksiniz. Bu kutsal yapı mimaride Altın Oranın güzel bir örneğidir.
Altın Üçgen Örneği: Büyük Giza Piramidi
Altın Oran, Altın Dikdörtgen ve Altın Üçgen, Dünyanın Yedi Harikasından biri olan Büyük Giza Piramidi'nin mükemmelliğinde bulunabilir. Altın Oranı bulmak için piramidin kare tabanını yarıya indirmeniz ve piramidin merkezine doğru dikey bir çizgi çizmeniz gerekir. Bu piramidin açılı bir tarafına bağlandığında 1.618 oranı olan Altın Oran olan Altın Üçgeni nasıl oluşturduğunu rahatlıkla görebilirsiniz.
Diğer Mimari Örnekler
Antik ve modern kutsal mimarinin ve Altın Oran binalarının birçok örneğini bulabilirsiniz.
- Chartres Katedrali - Merkez, Fransa
- Notre Dame - Paris, Fransa
- Bakireler Sundurması - Akropolis, Atina
- Tac Mahal - Agra, Hindistan
- Birleşmiş Milletler Binası - New York City, New York
Sanat Örneklerinde Altın Oran
Altın Oranı kullanan usta ressamların pek çok örneğini bulabilirsiniz. Bu mükemmel eserler Altın Dikdörtgenler ve Altın Üçgenlerin oranı kullanılarak oluşturulmuştur. Altın Dikdörtgen temel alınarak oluşturulan sanatın insan gözüne daha hoş geldiği kanıtlanmıştır. Bu mükemmel dikdörtgeni ve Altın Oranı çevreleyen gizemlerden biri de bu.
Sanatta Altın Oran

Altın oran sanatı örnekleri şunları içerir:
- Leonardo Di Vinci - Mona Lisa, Vitruvius Adamı
- Botticelli - Venüs'ün Doğuşu
- Michelangelo - Kutsal Aile, 'Davut'
- Raphael - Çarmıha Gerilme
- Rembrandt - Otoportre
- Salvador Dali - Son Akşam Yemeği Ayini, Hafızanın Kalıcılığı
Sanat Kompozisyonunda Altın Oranın Kullanımı
Altın Dikdörtgenin içinde görsel olarak diğer alanlara göre daha çekici bulunan belirli alanlar vardır. Bu noktalar, dikdörtgenin alt köşesinden karşı köşeye bir çizgi çekilip diğer alt köşede tekrarlanarak keşfedilir. Bu çizgiler Altın Dikdörtgenin tam merkezinde kesişecektir. Daha sonra, merkez noktadan başlayarak her çizginin ortasını ölçün. Bu dört noktaya dikdörtgenin gözleri (Altın Oran) denir. Daha sonra resmin ana odak noktası bu ilgi noktaları (oranlar) dahilinde çizilir veya boyanır.
Müzikte Altın Oran

Müzik sayısal değerlerden oluşur ve bir müzik eseri oluşturulurken Altın Oran kullanıldığında matematiğin canlı bir örneği haline gelir. Fibonacci Dizisi müzikte de yaygındır:
- Bir gamda sekiz nota vardır.
- Üçüncü ve beşinci notalar akorların temelidir.
- Herhangi bir notanın uzunluğu veya oktavı 13 notadır.
Sıralama bir müzik parçası boyunca devam eder ve Altın Oran'a ulaştıkça daha karmaşık hale gelir.
Altın Oranı Kullanan Besteciler
Bach, Beethoven, Chopin ve Mozart gibi en bilinen klasik bestecilerden bazıları müzik parçalarında Altın Oran ve Fibonacci Sıralamasını kullandı. Casey Mongoven gibi bazı modern besteciler müziklerinde Altın Oranı araştırdılar.
Doğadaki Altın Oran Örnekleri

Doğada Altın Oran nerede bulunur? Altın Oran kullanılarak oluşturulabilen Altın veya Fibonacci Spiralindedir. Bu, doğal dünyada yaygın olarak bulunan bir olgudur. Bir bitkinin yaprakları mümkün olduğu kadar çok büyür ve gövdeye doğru spiral çizebilir. Yeni bir yaprak, ancak kendisinden sonraki yapraktan sonra oluşur.
- Sarmal kaktüsler
- Sarmal galaksiler
- Ayçiçekleri
Fibonacci Dizili Çiçekler
Bazı çiçeklerde Fibonacci Sırasını takip eden çiçek yaprakları bulunur:
- Üç yaprak:İris, zambak, orkideler, trillium
- Beş yaprak: Düğün çiçekleri, sardunyalar, ebegümeci, sabah sefası, nasturtium
- Sekiz yaprak: Delphiniums
- 13 yapraklar: Bazı papatya çeşitleri, kanarya otu, kadife çiçeği
Çam Kozalakları'ndaki Fibonacci Spirali

Ağaç türlerine bağlı olarak, çam kozalaklarında da Fibonacci sayı dizisinde Altın Oranın işleyişini görebilirsiniz. Çam kozalağının bir tarafında sekiz adet spiral, diğer tarafında ise 13 adet spiral bulunmaktadır. Başka bir çam kozalağı deseninde bir tarafta beş, diğer tarafta sekiz spiral bulunur.
İnsanlarda Altın Oran
Bu oran sadece insanların birbirlerini nasıl gördükleri açısından değil, aynı zamanda vücutlarının nasıl çalıştığı ve DNA'ları açısından da önemlidir.
DNA Altın Oranı Ortaya Çıkarıyor
Altın Oranın en muhteşem örneklerinden biri insanın DNA yapısında bulunmaktadır. Bu, DNA çift sarmalının ongen şeklini oluşturduğunu ortaya koyan tek bir DNA kesitinde görülebilir. Bu, birbirinden 36 derece döndürülmüş iki beşgenin birleşimidir ve DNA çift sarmalını oluşturur. Çift sarmal spiralin kendisi bir beşgen oluşturur. Tek bir DNA molekülü bile Altın Oranın veya İlahi Oranın temelini açığa çıkarır.
Altın Oranın Arkasındaki Matematik
Altın Oranı gerçek hayatta bulmak, etrafınızda göründüğü için basittir. Bu, doğada bulunan ve insanlar tarafından yüzyıllardır kopyalanan ve taklit edilen, yaygın olarak mükemmel sayı olarak bilinen sayıyı tanımlamak için kullanılan matematiksel bir gerçektir. Bu sayının basit güzelliği, uygulamadaki karmaşıklığını gizliyor. Altın Oranın ardındaki teoriyi anlamak için öncelikle oranın Fibonacci Sıralamasını incelemelisiniz.
Fibonacci Dizisi ve Altın Oran
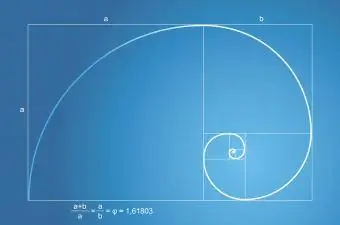
Fibonacci Dizisi veya Dizisinin Altın Oran ile ilişkisi vardır. Fibonacci Serisi, bir bitkideki yaprak sayısında ve bir çiçekteki yaprak sayısında ortaya çıkar. Doğada bulunan Fibonacci Spirali her zaman Altın Oranlı bir Altın Dikdörtgenin parçasıdır.
Fibonacci Serisinin matematiği basittir:
- Sıra 0 ve 1 ile başlar.
- Serideki bir sonraki sayıyı elde etmek için son iki sayıyı toplamanız yeterli.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 vb.
- Bu Fibonacci Dizisi örneği şöyle olur: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, vb.
Fibonacci'nin Altın Oran ile ilişkisi ileri, ileri ve ileri eklendiğinde ortaya çıkar. Seriyi ne kadar çok eklerseniz Altın Oran'a o kadar yaklaşırsınız.
Altın Dikdörtgen ve Üçgen Oluşturma
Fibonacci Dizisi ile Altın Dikdörtgen oluşturmak için bir kareyle başlarsınız. Orijinal kareye bir kare daha ekleyerek bir dikdörtgen oluşturmaya başlayacaksınız. Formülü kullanmayı unutmayın: 0+1=1 ilk karedir, 1+1=2 - başka bir kare ekleyeceksiniz.1+2=3'e üç kare ekleyeceksiniz ve ardından 2+3=5'e beş kare ekleyeceksiniz. Kareler eklemeye devam edecek ve sonunda bir Altın Dikdörtgen oluşturacaksınız.
Altın Dikdörtgeni bir köşeden diğer köşeye ikiye bölerek Altın Üçgen oluşturulabilir. Bu, üç tarafının veya açısının 2:2:1 oranında olduğu bir üçgen oluşturur; bu, iki uzun kenarın uzunluğunun eşit olduğu ve kısa açının uzunluğunun iki uzun kenarın tam yarısı olduğu anlamına gelir.
Gerçek Dünyada Altın Oran
Altın Oran, doğadaki ve insan vücudundaki önemi nedeniyle sıklıkla İlahi Oran olarak anılır. Altın Oranın pek çok canlıda mevcut olduğunun keşfi, bu büyülü orana duyulan saygıyı artırdı ve bugün sanatçılar ve yaratıcılar için ilham kaynağı olmaya devam ediyor.






